Oscillators are designed with amplitude, frequency and phase stability in mind.
However, the signals of the circuits described here are not stable neither cyclic
since they implement chaotic dynamic equations as voltage variations.
Their 3 outputs can be seen as the coordinates of a point in a phase space,
and a 2D view of the trajectory can be displayed on a XY oscilloscope.
Frequency response of these signals are also of interest.
Of course any software would display these attractors in full 3D and nice colors,
with no hardware at all except a computer - but hey, where's the fun then ?
The top menu links to pages showing equations, full schematics
of the electronic circuits, plots of all the output's time series,
Fourier Transform, and parametric phase space attractors.
In practice we use equations to solve physics problems :
here we will use analogic circuits to solve dynamic equations,
which is easily done by the use of common off-the-shelve AOPs.
The retrieval of V from the dv/dt variation uses an RC integrator.

Roughly, feeding dv/dt at the input gives -V at the output.

Addition, substraction, multiplication by a constant and
weighted sums are performed using one or more summing AOP.

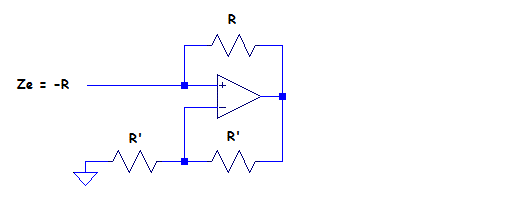
Negative resistor by the means of a Negative Impedance Converter.
The product of two voltages can be implemented using log and exp converters,
however for a simpler design we will use an analogic multiplier like the AD633.

Now we have everything in hand to build our chaotic oscillators :
check the top-page menu for Lorenz, Rossler and Chua circuits.